To our knowledge, the throughput of our system versus angles has not previously been accounted for. To determine it, we placed the teflon cap in the sample chamber, submerged it in water and put a square coverslip on top, just as we would for a bead sample. The scattergram for the cap is shown below.
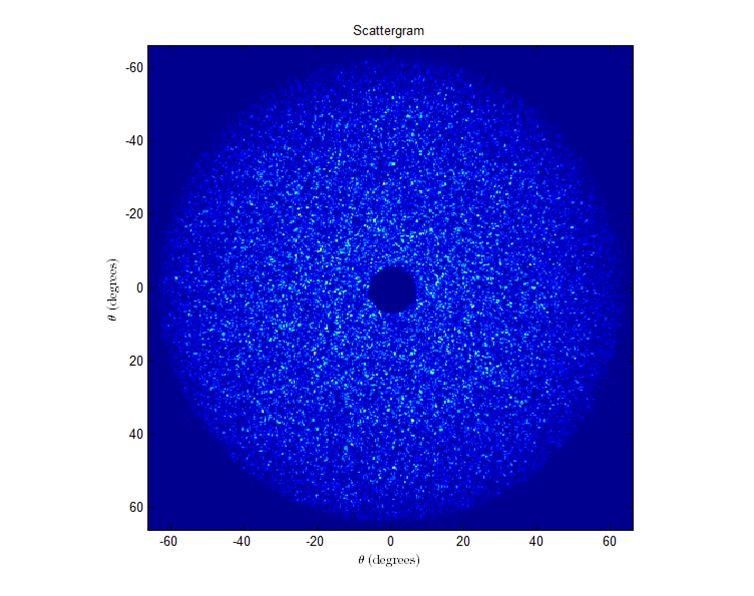If the throughput did not change versus angle, then the intensity should be about constant (with noise) throughout the entire scattergram.
However, we can tell from the cut-throughs that there is indeed a falloff. This falloff can be well fit to a cos(theta) function: Throughput(θ)=I(θmin)cos(θmin)cos(θ)
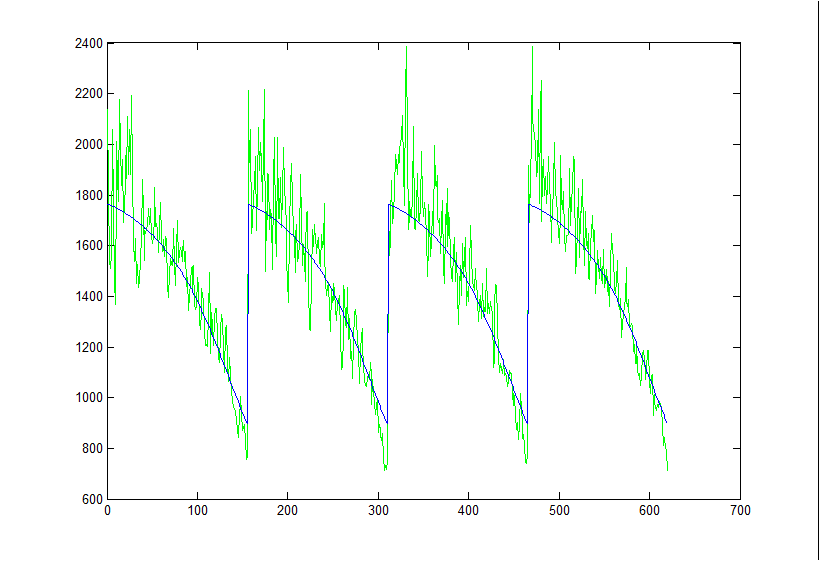Here is the least squares fit to a 5um bead without any throughput correction:
And here is the fit with the throughput correction. The theory cut-throughs were multiplied by the above throughput equation and then least square fit to the data (with an offset and stretch term).
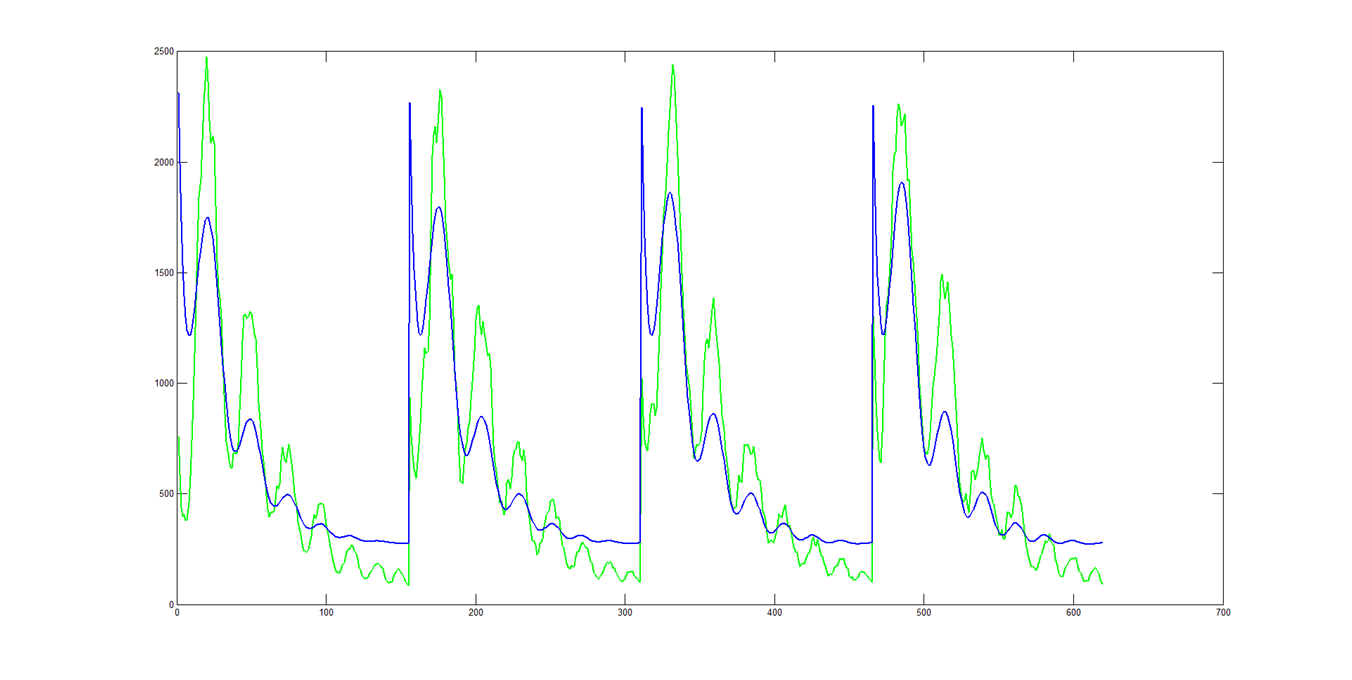The throughput correction did not have much of an impact on the quality of the fits. If instead you LSF the theory cuts to the data, like normal, and then multiply by cos(θ):
The amplitudes of the peaks are still to small, but the falloff trend seems more correct.